Al igual que en un par de post anteriores, donde publiqué los códigos de métodos de calculo de raices de ecuaciones no lineales en matlab, ahora los publico de nuevo, pero esta vez adaptados a Scilab:
Método de la Bisección: biseccion(inicio,fin,%error);
Método de la Regla Falsa: reglafalsa(inicio,fin,%error);
Método de Newton-Raphson: newtonraphson(inicio,%erro);
Método de la Secante: secante(inicio,fin,%error);
Método de Iteración del Punto Fijo: puntofijo(inicio,%error);
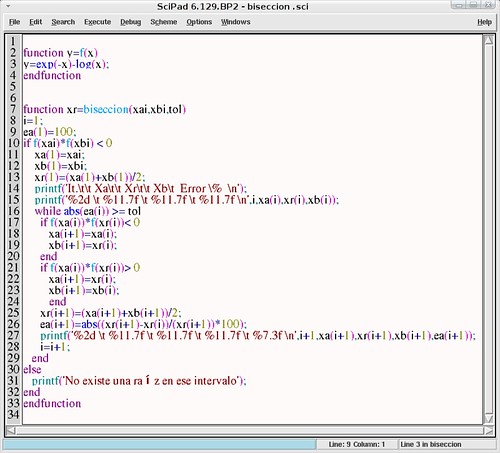
Pueden guiarse viendo el ejemplo de ejecución del código del método de la bisección:
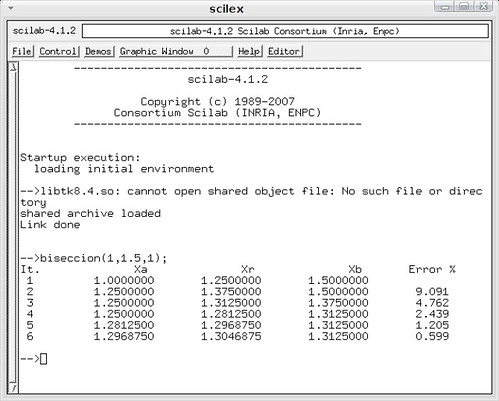
Para ejecutar el programa, guardar el código editado con SciPad como ‘biseccion’, ejecutarlo (control + l) y llamar a la función desde el Scilex:
Nota: Los códigos vienen establecido con una ecuación por defecto en la función f, df (derivada de f) y g. Pueden modificar la ecuación por el que deseen analizar.
I don’t think the title of your article matches the content lol. Just kidding, mainly because I had some doubts after reading the article.
Thank you for your sharing. I am worried that I lack creative ideas. It is your article that makes me full of hope. Thank you. But, I have a question, can you help me?
Thank you for your sharing. I am worried that I lack creative ideas. It is your article that makes me full of hope. Thank you. But, I have a question, can you help me?
Your article helped me a lot, is there any more related content? Thanks!
muchachos alguien me puede mandar el codigo del metodo de newtonrapson bien sencillo
Hola quisiera preguntar como se podria graficar esto???
por favor, como
por favor, como para ingresar un .txt en este archivo, lo ejecuto y tengo este error
.sce:’,’directo.sce’)
!–error 77
string: Wrong number of input argument(s): 1 expected.
at line 15 of exec file called by :
exec(‘G:\geofisica\geofisica.sce’, -1)
//entrada de datos
archivo=string(‘ESCRIBA EL NOMBRE DEL ARCHIVO DE DATOS INCLUYA LA EXTENSIÓN .sce:’,’directo.sce’);
arch=load(archivo);
[filas columnas]=size(arch);
F=arch(:,1);
C=arch(:,2);
noce
Muchas gracias por los ejemplos, fueron de mucha ayuda ya que ahora mismo estoy practicando los mismos temas.
Quería hacer un pequeño aporte.
Para hacer general los métodos, sería útil poder pasarles las funciones como parámetros.
Esto lo hacemos definiendo la función afuera (en el intérprete):
Por ejemplo:
deff(‘[y] = f(x)’,’y = x^2′)
Y luego llamamos al método con:
biseccion(f,a,b,error)
y dentro de la funcion simplemente hacemos f(a) o f(b) según corresponda.
Esto le agrega mucha generalidad al procedimiento 😉
Acá va un código de ejemplo con Newton-Raphson, donde le paso la función y su derivada como parámetro:
// CALCULA f(x) = 0 con el Método de Newton-Raphson
//
//Datos:
// f : funcion a calcular el 0
// fp : f’, derivada de f
// p0 : Aproximación Inicial
// tol : mínima tolerancia
// maxit : cantidad de iteraciones máximas
//
//Iteración k-ésima:
// p(n) = p(n-1) – f(p(n-1))/fp(p(p-1))
//
//Devuelve en r la historia del residuo
function [p,it,r] = newton(f,fp,p0,tol,maxit)
r = zeros(1,1);
for i = 1:maxit
it = i; //actualizo iteraciones
p = p0 – f(p0)/fp(p0); //calculo proxima iteracion
r = abs(p – p0); //calculo residuo
r = resize_matrix(r,size(r,’r’)+1,size(r,’c’)); //agrego una nueva fila a la historia
r($,:) = abs(p – p0) //completo la fila
if (r($,:) >= tol) then //condicion de corte
return
end
p0 = p; //actualizo p0
end
disp(«Maximo de iteraciones alcanzadas»);
endfunction
Gracias por el aporte fern, me gusta cuando las personas mejoran lo que hago…
saludos!!!!
Hola, tengo un problema, tengo una ecuacion no lineal con dos soluciones, 0 y 0.0075, el problema que tengo es que siempre el metodo de la secante y el de newton me devuelven la solucion 0. Como podria hacer para encontrar las dos soluciones?
Muchas Gracias
Ignacio
ea= error absoluto 🙂 torpe tavo jejeje
muy bn aporte men.!!!!!!
no entiendo que es ea, es una bandera???
gracias por el aporte..
exitos
=)
de casualidad tu no tienes el codigo en scilab de las series de taylor maclaurin y laurent para que tambien los publiques los necesito gracias….
¡Muy buen aporte, mereces un 10!
Muchas gracias por compartir con nosotros estos códigos para Scilab. La filosofía del software libre es la generosidad.
Éste es el código de la linea 27:
printf(‘%2d \t %11.7f \t %11.7f \t %11.7f \t %7.3f \n’,i+1,xa(i+1),xr(i+1),xb(i+1),ea(i+1));
%2d (enteros – tamaño de separacion = 2)
%11.7f (punto flotante – el tamaño de separación es 11 y tiene 7 decimales – ejemplo: x.0000000)
%7.3f (punto flotante – el tamaño de separación es 7 y tiene 3 decimales – ejemplo: x.000)
el \t es tabulación y \n salto de linea.
tiene 5 parámetros: %2d %11.7f %11.7f %11.7f %7.3f
por lo tanto debe tener 5 salidas:
i+1, xa(i+1), xr(i+1), xb(i+1), ea(i+1)
el resultado lo puedes ver en la imágen inferior al código, y como te darás cuenta:
%2d (It) muestra enteros
%11.7f (Xa) tiene 7 decimales
%11.7f (Xr) tiene 7 decimales
%11.7f (Xb) tiene 7 decimales
%7.3f (Error %) tiene 3 decimales
El espacio de separación puedes percibirlo.
La linea 14 es la que me muestra los títulos, y se ejecuta una sola vez, ahi no mando variables de salida, solo imprimo una cadena y considero parámetros de tabulación como también un salto de linea
Saludos!!
hey podrias explicar por favor los argumentos que entrar en la funcion printf??????????????’
😉 ta weeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeno pero deberias explicar el codigo=)